(1)多項式の展開を用いる教材 最初に,多項式の展開を用いる教材について考 察する。組合せからの準備として,「表1」にあ るような問題プリントから始めることとする。 表1 整数 問題プリント1 問題1 pを素数,rを1 r p 1である自然数とす る。このとき, p Cこの無限小数のような式をF2形式べき級数と言い、 右辺を左辺の形式べき級数展開という。 定理:定数項が1で次数nのF2多項式f(t) = tn 1に 対し、1=f(t)のべき級数展開の係数は循環し、 周期は2n 1以下。 周期は1 = tP mod f(t)となる最小の自然数P 1。く適切な重みに基づいた直交多項式をとる方が, 領域内での多項式の値を低精度の数値係 数を用いても平均的に良く近似できるので有利であろう このような立場に基づいた考察 を試みる 1 導入 数値係数多項式の代数的処理を数値的に扱うことを試みる 今回,

中3 展開と因数分解3 多項式と単項式のいろいろな計算 予習 中学数学の勉強に
多項式の展開 大学
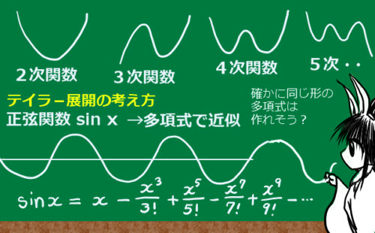
多項式の展開 大学-中学校 数学 京都教育大学の学生さんたちが作成された動画の数々です。 3分程度で、内容をコンパクトに説明してくださっています。 幅広い内容が扱われているので、きっと皆さんのお役に立つはず! (西岡加名恵、年5月9日) 文字「x」って何F ( k) ( a) ( x − a) k という多項式で近似できます。 (ただし、右辺は収束することが条件です。 ) また、 a = 0




中学数学2年 単項式と多項式とその次数 受験の月
テイラー多項式・マクローリン多項式 関数 \(f(x)\) の1次近似式を作るためには,導関数 \(f'(x)\) が存在しなければなりません。 さらに,2次近似式を作るためには,2次導関数 \(f''(x)\) が存在しなければなりません。 それでは,関数 \(f(x)\) が3階,4階と微分可能であれば, \(f(x)\) を3次や4次の数学Ⅰ eテレ 毎週 月曜日 午後2:10~2:30 ※この番組は、21年度の新作です。 多項式の基本6|3次以上の展開と因数分解の公式の総まとめ 前々回の記事で説明したように,たとえば x 2 − 2 x − 2 = 0 のような簡単には因数分解できない2次方程式は,いったん解を求めることによって因数分解できるのでした. では,3次式では因数分解
これらの条件をみたす多項式 Q, R の組は必ず存在高校講座home >> 数学Ⅰ >> 第2回 数と式 式の展開;また、直交多項式の積分の範囲が有限であるチェビシェフ多項式やルジャンドル多項式は大学入試の数学問題にも出やすいが、 ラゲール多項式は積分範囲が 0 から `oo` なので、大学入試の試験問題で出ることはまずないだろう。 さて、ラゲール多項式の
F ″ ( a) ( x − a) 2 ⋯ = ∑ k = 0 ∞ 1 k!東海大学紀要 情報通信学部 Volxx, Noxx , xx, ppxxx xxx ― 1 ― 大学初年次における数学教材の提案(その) ~ヘヴィサイドの展開定理~ 貴田 研司*1 A Suggestion on Mathematical Materials for Freshman Education Vol ~ Heaviside Expansion Theorem ~ by Kenshi KIDA*1 多項定理 (abc) n の展開式の係数 二項定理をさらに一般化し,\ 三項以上にまで拡張する \\ 2zh 二項定理では,\ 「組合せ」の考え方を用いて\ $ (ab)^n$の展開式を得た \\ 2zh 同様に考えても拡張は可能だが,\ 式が複雑になってしまうので別の考え方で




中学数学 多項式 の教え方 展開の基本



1 Sinxの有限マクローリン展開を第4項まで表せ 2 Tan Yahoo 知恵袋
また、展開公式の複 数の証明方法を挙げる。最後に、この展開公式の動機である対称性破れ作用への応用に ついて触れる。 1 主結果 最初に、Gegenbauer 多項式の定義と性質を復習する。Gegenbauer 多項式 y=C_{n}^{ $\lambda$}(x) は 2階の常微分方程式多項式の展開 Date07年11月16日 分配法則と展開公式①(中学範囲) : 説明 ・ 例題 ・ 練習問題 展開公式②(3乗の展開公式): 説明 ・ 例題 ・ 練習問題About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ




中学数学2年 単項式と多項式とその次数 受験の月
ベーシック数学 eテレ 毎週 月曜日 午後2:00〜2:10 ※この番組は、前年度の再放送多項式カーネル • 特徴量ベクトル (2次元3次多項式) • 多項式カーネル – 3次多項式カーネル – m次多項式カーネル • カーネルトリック 筑波大学 情報科学類 19年度講義資料 (機械学習) 11ラゲール多項式の積の展開公式 II 高 橋 光 一 任意の指標の二つのラゲール多項式(Laguerre's polynomials)の積を和に展開する新しい 公式を提示する。 1 ラゲール多項式 ラゲール多項式は,区間 における重み付き直交性をもつ多項式の一種である。 すなわち,
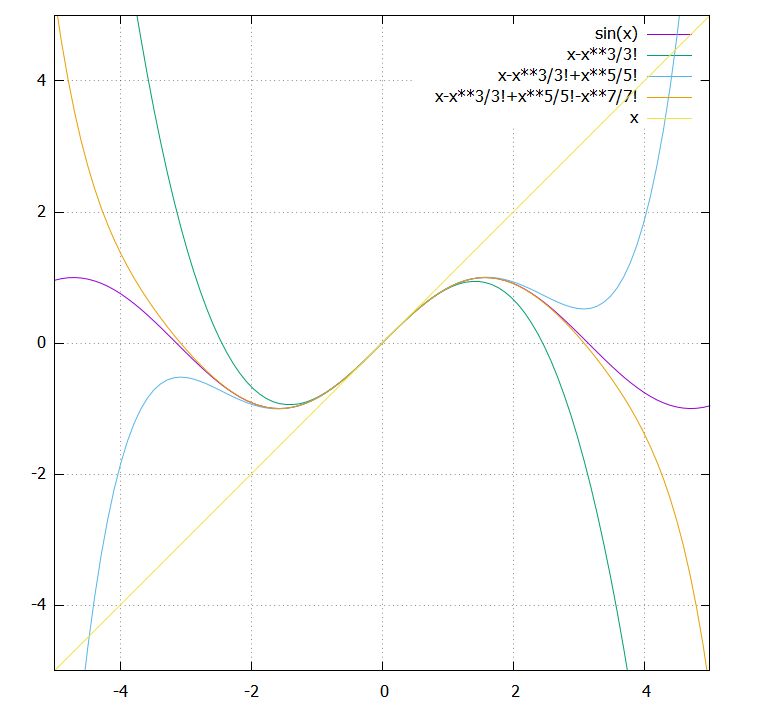



なぜテイラー展開を学ぶ 単振り子を例にわかりやすく解説 趣味の大学数学




高校数学 多項定理 A B C Nの展開式の係数 受験の月
三宅 克哉 早稲田大学, 総合研究機構, 教授 () 非アーベル的現象の探索法を探って, 一般次数対称群に対する生成的多項式の同型問題への方法を理論的に構築し, 「特殊化」によって活用する手法を確立した さらに5次までの可解群に対する生成的多項式高校講座home >> ベーシック数学 >> 第11回 2次方程式 式の展開;直交多項式による展開は,全 体的近似と呼ばれてお り,あ る範囲全体での多項式近似がテーラー展開に比 較してはるかにすぐれているのである簡 単な例で説 明する 2 指数関数の場合 変数aの 指数関数のテーラー展開はよく知られて * 原稿受付 昭和60年2月12日




数学 多項式の係数を求める問題 展開 大学入試数学の考え方と解法
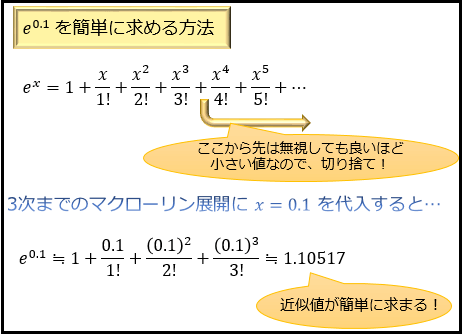



テイラー展開 マクローリン展開はどう使うのか 関数をシンプルに考える近似のテクニック アタリマエ
ルジャンドル多項式の計算 ルジャンドル多項式 P n (x) (n = 0, 1, 2) P_n(x)\(n=0,1,2) P n (x) (n = 0, 1, 2) を直交性を用いて導出してみます(漸化式を用いる方が楽ですが,多項式の直交性について理解を深めるためにあえて直交性を用いてやってみます)。物理のための 応用数学 小出昭一郎・阿部龍蔵 監修/ 元 明治大学教授 理博 小野寺嘉孝 著 A5判/236頁/定価2970円(本体2700円+税10%)/19年3月発行 ISBN (旧ISBN ) C3042 理工系の学生が大学2年から専門課程で主として物理を学ぶ131 100,正規直交完全系 72,超関数 77,Dirichlet積分 CauchyRiemannの 関係式 Coulombの法則 Eulerの公式 Fickの法則 Fourierの積分定理 Fourier変換 Fourier展開係数 Fourier級数 Fourier級数展開任意の区間複素係数(complex coefficient) Fourier級数展開定理(Fourierseries expansion theorem) 14 Fourier多項式 Fourier級数展開任意の区間複素



服部嗣雄 難問題の系統とその解き方 新課程 物理 の活用法と歴史




式のかけ算の筆算 数学の偏差値を上げて合格を目指す
多項式関数を関数値から決定する 諸アルゴリズムの比較 野崎昭弘 サイバー大学it総合学部・教授 1 多項式関数の決定とは a 問 題 与えられた観測データから理論式のパラメータを決定する問題は,理論式が 次多項 式である場合には,次のように述べられる。1W数学演習II 標準H0021 担当教員 浜中真志 研究室 A327 Emailhamanaka@mathnagoyauacjp 1変数関数のテイラー展開 作成日 Updated Version 10 実施日 今回から微分積分の話題に入ります.まずは前期の復F ′ ( a) ( x − a) 1 2!




乗法公式 多項式の展開公式 の覚え方と使い方 数学fun




式のかけ算の筆算 数学の偏差値を上げて合格を目指す
次に,これらの展開式が成立することを示しましょう.まず,よく出題される大学入試問題を少し書き直したものを解きます.なお,nは(任意の)正の整数とします. 問題2.2 f(x)を何回でも微分可能な関数とする. とおくと,多項式の除法とは、体 K 上の(1変数)多項式 f, g (ただし g ≠ 0 )に対して、次の2条件をみたす多項式 Q, R を求める手続きである。 f = gQ R; テイラー展開(Taylor expansion)は、大学の微積分学のメイントピックのひとつです。 しかしながら、教科書に書いてある展開式が複雑で、覚えられない。何に使うのか、どんな意味があるのか、なぜ学ぶのだろうか? 今回は、単振り子の運動、三角関数(サイン)を例に、テイラー展開




Expansion Factorization 式の展開と因数分解 Math In English 4 Okenavi




多項式の係数の和の求め方とは 大学入試数学の考え方と解法
電301 数値解析(17) 琉球大学工学部電気電子工学科担当半塲 10 関数近似とは何か(10) • 三角関数以外で, もっとも一般的なのは, 多項式 を使った展開である 関数のTaylor 展開は多項 式エルミート多項式による一般フーリエ級数展開のいくつかの例 関西学院大学大学院理工学研究科 数理科学専攻 示野研究室 藤井 都 直交多項式の1 つであるエルミート多項式による一 般フーリエ級数展開の実例について得た結果を述べる.¶エルミート多項式. 次の関係式: φ(x)hj(x) = (−1)j dj dxj φ(x) を満たす多項式hj(x)をエルミート多項式という. µ コーニッシュ・フィッシャー展開 冒頭の仮説検定問題では%点を求める必要がある.最後にこの求め方に触れる.wα をSn の上側α%点,zα を標準正規分布の上側α%点とする.この




テイラー展開の復習




第1回 京都大学 1997年 数学 理系 後期 京大生が選ぶ感動した一問 受験対策 京大塾
テイラー展開の公式 まずは公式を紹介します。 x が a に近いとき、 f ( x) = f ( a) 1 1!R の次数は g の次数よりも小さい。 (ただし、定数多項式 0 の次数は 0 より小さいものと解釈する。;定理(Abel) n 5の場合,一般にはn次方程式の根を方程式の係数から加減乗除とべき根 をとる操作のみを用いて求めることはできない. この定理は16年の論文でAbelにより証明されました. 17 根の個数 定理13を用いると,複素数係数のn次多項式 f(x) = xn a n 1x n



テイラー展開 をわかりやすくまとめてみた おすすめ動画あり もんプロ 問題発見と解決のためのプログラミング
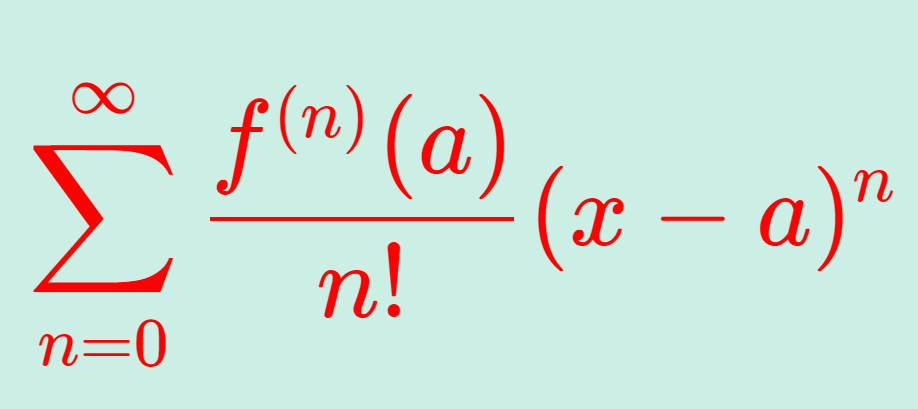



テイラー展開 マクローリン展開とは 解析的な関数と具体例 数学の景色
Zernike 多項式を用いて解くことができる。Zernike 多項式は、単位円上の完全直交関数系 なので(115)、どのような連続関数に対しても、そのZernike 展開は最小自乗近似(L2 ノ ルム1の最小化) になっている 。 ここで、回転対称性から、この近似は 2n 次の回転 この無限級数を途中で打ち切ったものは多項式になります。つまり, マクローリン展開を用いると,一般の関数 f (x) f(x) f (x) を多項式で近似することができる。その多項式は, f f f の x = 0 x=0 x = 0 における高階微分係数から定まる と言えます。Ex , sinx , cosx について, x = 0 の周りの近似式としてマクローリン多項式について理解します。 マクローリン展開からオイラーの公式 eix = cosx isinx を導きます。 線形2階斉次微分方程式 y ″ ay ′ by = 0 ⋯ ( ♪) について,特性方程式が相異なる実数解



数と式の問題 Of 京極一樹の数学塾会員頁




フーリエ級数展開 その1 大学数学物理簡単解説
算数・数学科 算数・数学を活用して,協働的に問題を解決しようとする子供の育成 HUEcompulsory education school 1.単元名 1章 多項式 2.単元の目標 単項式と多項式の乗法,多項式を単項式で割る除法,一次式の乗法,乗法公式を用いる式の展開や因数分解について, (1)問題概要 (abc)ⁿなど3項以上の展開式のある項の係数を答える問題。 (2)ポイント 多項展開式の一般項を使いましょう。 また、rの値が見てすぐに分からないときは、rを含んだ方程式を立てます。 その際、指数法 "多項展開式"の続きを読む 定理は、もっと実用的で、定義などを組み合わせて、便利に論理をスキップできるツールです。 よって高級言語的な立ち位置かな。 nを非負整数とし、最高次係数が2^ (n1)で次数がnとなる整数係数多項式をTn (x) とする。 各n,mでTn (Tm (x)) =Tm (Tn (x)) をみたす




テイラー展開



1
多項式の次数の日本語名称は、一貫して次数の値に接尾辞「次」をつける。英語名称は、いくつかの例外はあるが基本的にラテン語の序数詞に形容詞を作る接尾辞の ic を付けて表す。 次数と不定元の数はきちんと区別されるべきであって、こちらには接尾辞「元」あるいは「変数」を付ける乗法公式は、式の展開を簡単にできる公式です。 それぞれの公式の左辺を展開すると、右辺になります。 一つずつ見ていきましょう! 乗法公式「平方タイプ」 ひとつの多項式の2乗、つまり平方の形になっている場合です。




多項式 127kb




中学数学3年 単項式と多項式の乗法と除法 受験の月




因数分解を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに




数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




Twitter पर Mikiop Limを動かしてのとき分母が0になるとなんで分子も0になるのかなあと思って 高校数学の美しい物語で調べたらめっちゃ難しそうなの出てきて戸惑ってる




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学




第1回 京都大学 1997年 数学 理系 後期 京大生が選ぶ感動した一問 受験対策 京大塾




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学




中学数学 式の展開 因数分解




ある反転授業の試み 正規分布のtaylor展開をとおして
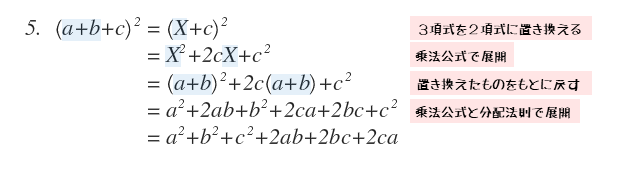



数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん




多項式の掛け算 展開 を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに




中学3年数学 3項式の展開 Youtube
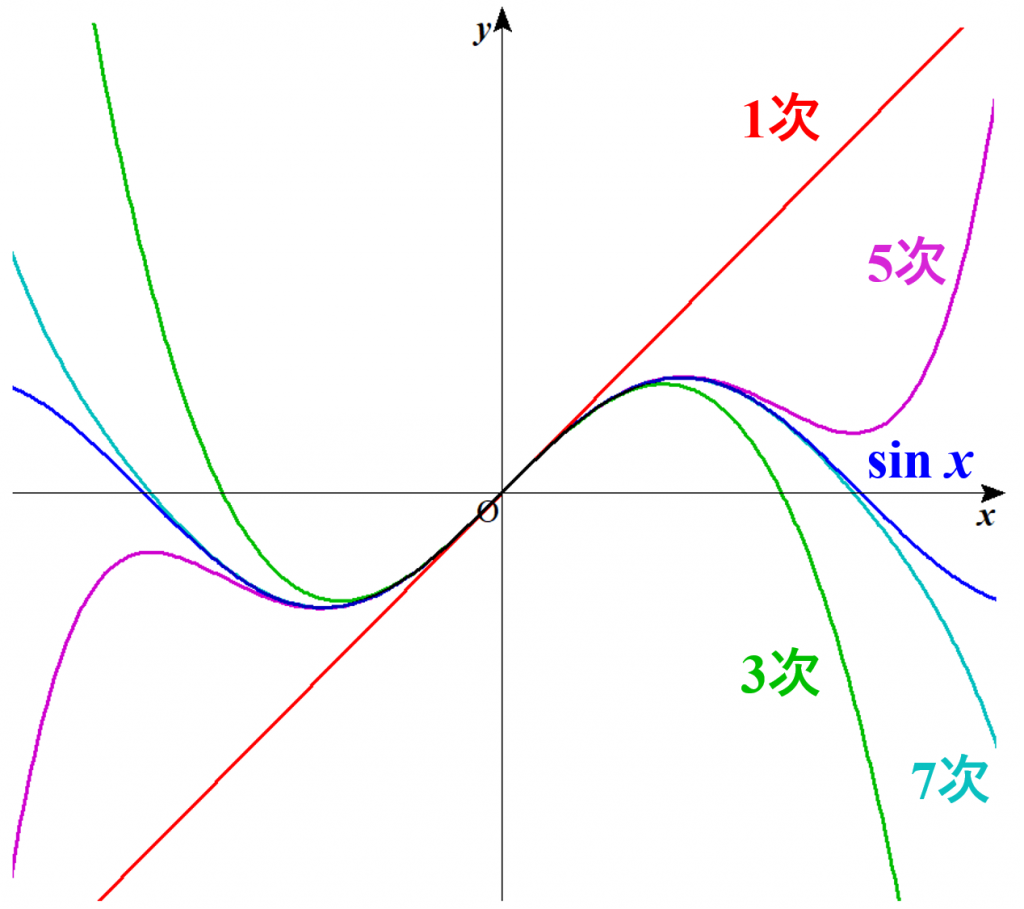



テイラー展開 の分かりやすい解説 理系のための備忘録
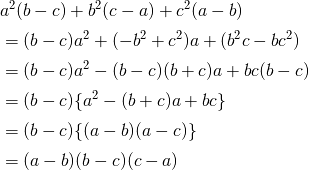



公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局



東大数学専科典型題演習34 マクローリン展開




授業実践記録 数学



1




連立多項式の近似根の計算法について 数式処理における理論と応用の研究
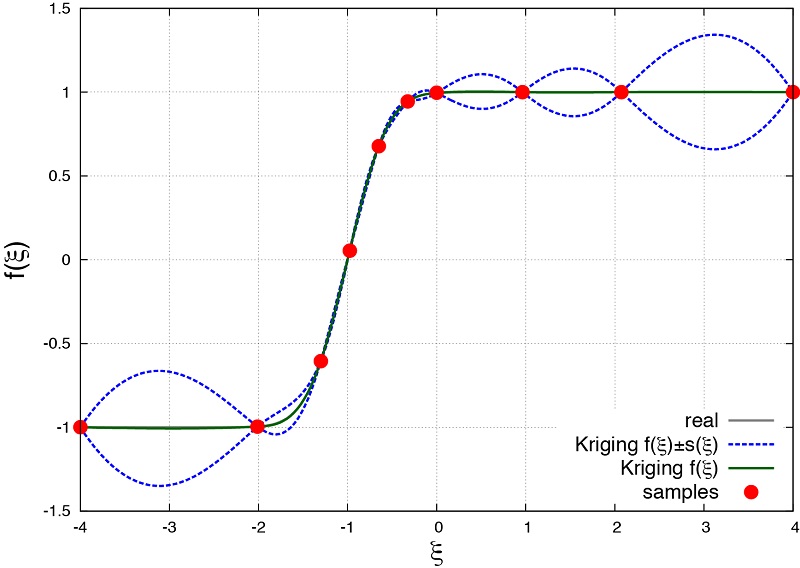



派遣研究者レポート 頭脳循環を加速する若手研究者戦略的海外派遣プログラム次世代流体科学の展開に向けた戦略的国際共同研究プロジェクト 東北大学 流体科学研究所




テイラー展開 1回目 テイラー展開とは関数を多項式で近似することです Youtube



Www Kurims Kyoto U Ac Jp Kyodo Kokyuroku Contents Pdf 1666 21 Pdf




数値多項式と関数空間 Computer Algebra Design Of Algorithms Implementations And Applications




微積分 テイラー展開とマクローリン展開 本質編




数学 B 多項式の割り算 自治医科大 明治薬科大 大学入試数学の考え方と解法




高校数学 マクローリン展開 関数の整式近似 とオイラーの公式 E Ix Cosx Isinx 受験の月



数学 中3 3 展開 4つの公式 Youtube




Expansion Factorization 式の展開と因数分解 Math In English 4 Okenavi




123 難関大学入試問題解説 18中央大学入試 数 多項式の展開 係数 数検1級 準1級 中学数学 高校数学 数学教育 Jjmo Jmo Imo Math Olympiad Problems Youtube



U9j580gf8iba369ji2w Xyz P 565




マクローリン展開の超解説 公式 証明 メリット 理系ラボ




大分大学 医学部 14年問題2 Suugaku Jp



U9j580gf8iba369ji2w Xyz P 565




部分分数分解の主要パターン おいしい数学




多項式の係数問題 必須だよー 中央大学18 金沢市 大学受験 はなぶさ塾 英塾 浪人 既卒 現役 高3 のブログ




中学数学 多項式と多項式の乗除 中学数学の無料オンライン学習サイトchu Su




夢ナビ 大学教授がキミを学問の世界へナビゲート




中学数学3年 展開と乗法公式 受験の月




3次以上の展開と因数分解はどうなる 公式の総まとめ
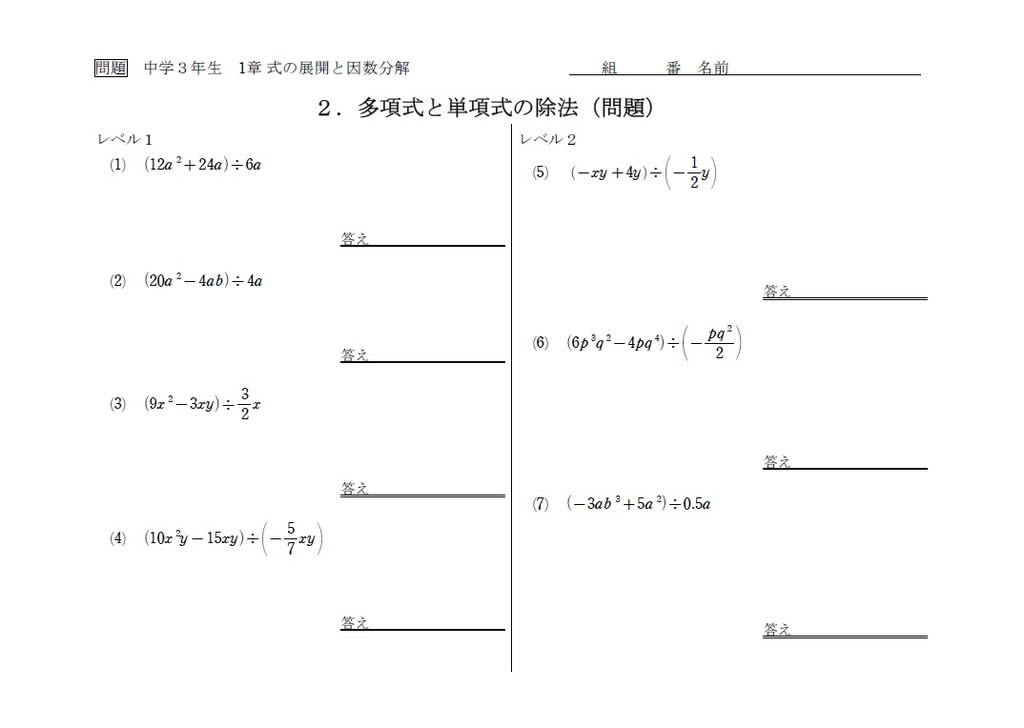



中3 展開と因数分解2 多項式と単項式の除法 予習 中学数学の勉強に
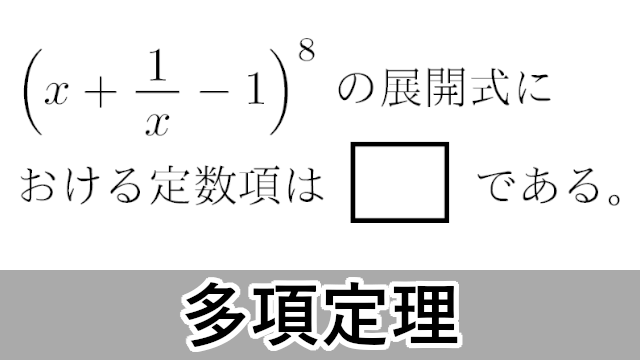



数学 B 多項定理 展開式の係数と定数項 北里大 愛知医科大 福岡大 大学入試数学の考え方と解法



Expansion Factorization 式の展開と因数分解 Math In English 4 Okenavi




三乗の公式 A B 3乗の展開公式と覚え方を解説



多項式の展開や因数分解を利用して 式の値を求めてください また多項式 Yahoo 知恵袋
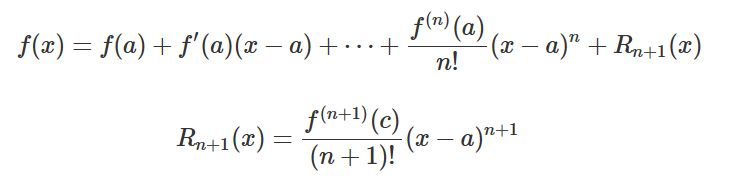



テイラー展開の展開式の覚え方 導き方 証明 趣味の大学数学



高階微分の応用 テイラー展開とマクローリン展開 理数系無料オンライン学習 Kori




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学




中学数学 多項式 の教え方 展開の基本




小学生でもわかる テイラー展開のきほん ついでにマクローリンも 理系大学生の数学駆け込み寺




上智大学 経済 経済 12年問題1 Suugaku Jp




テイラー展開 マクローリン展開はどう使うのか 関数をシンプルに考える近似のテクニック アタリマエ




数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ
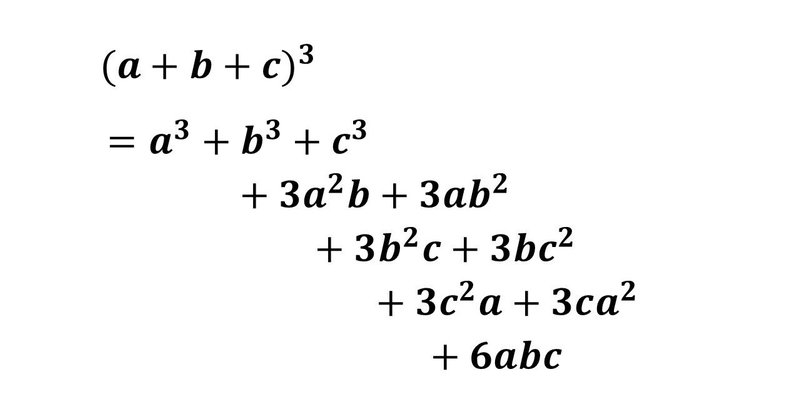



A B Cの2乗や3乗の展開公式 タロウ岩井の数学と英語 Note



服部嗣雄 難問題の系統とその解き方 新課程 物理 の活用法と歴史
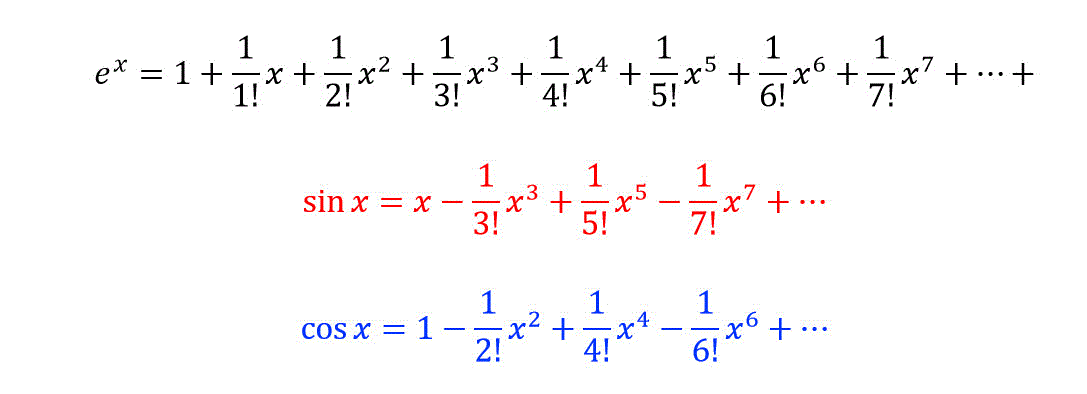



うさぎでもわかる解析 Part04 マクローリン展開 テイラー展開 工業大学生ももやまのうさぎ塾




中3数学 式の展開の公式 やり方についてわかりやすく説明しました 都立高校受験応援ブログ



1




テイラーの定理とその証明 おいしい数学




中3 展開と因数分解3 多項式と単項式のいろいろな計算 予習 中学数学の勉強に




中学数学 式の展開 因数分解




高1 代数 2 多項式の演算 大学数学風に 高校生 数学のノート Clear




中学3年数学 3項式の展開 勉強 Youtube スタディチューブ




裏技 展開を一撃 最速で計算するテクニック 超わかる 高校数学 Youtube




乗法公式 式の展開公式 19個まとめ 高校数学の美しい物語




受験直前 入試問題から学ぶ大学数学 数学 統計教室の和から株式会社




多項式の乗法公式を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに




乗法公式 多項式の展開公式 の覚え方と使い方 数学fun



数と式の問題 京極一樹の数学塾
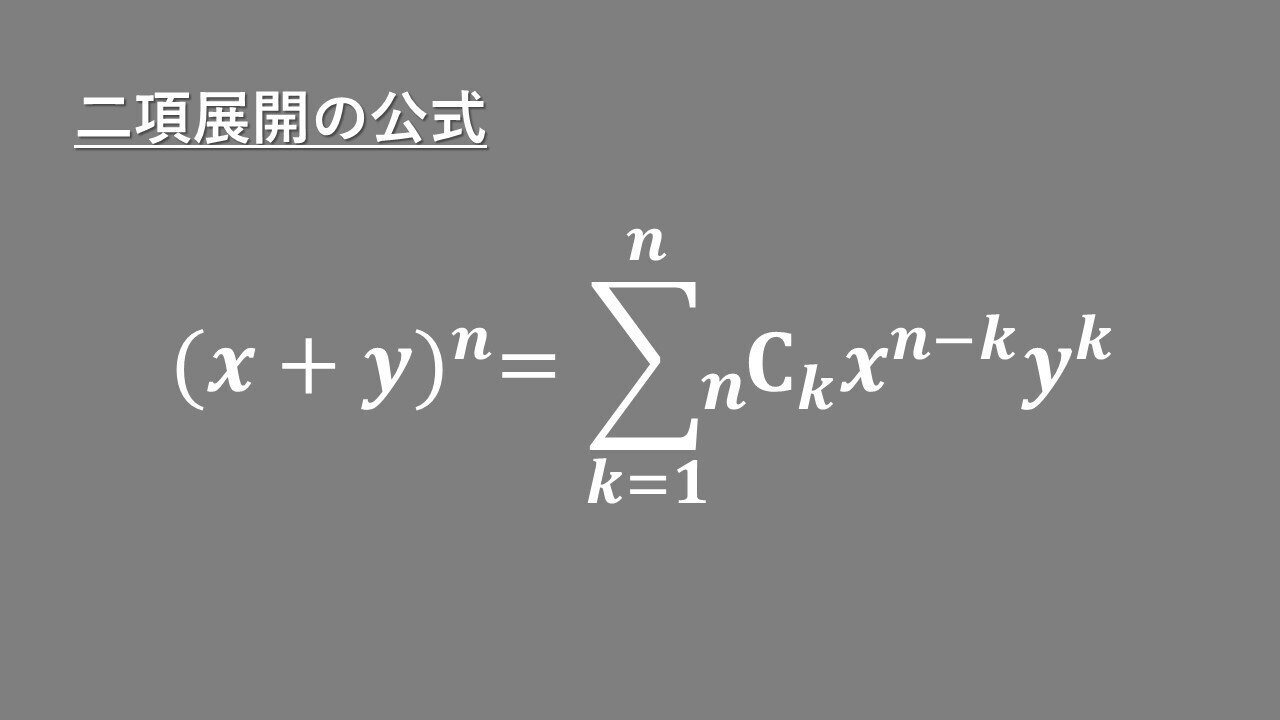



基本対称式の計算問題と二項展開 タロウ岩井の数学と英語 Note




テイラー展開とマクローリン展開 概要 オムニバスでまとめる大学数学 5 Liberal Art S Diary
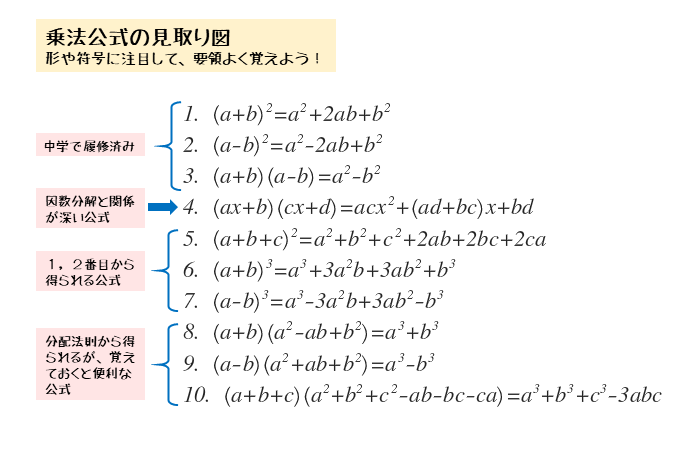



数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん



1




マクローリン展開の一部で挟まれた不等式の証明 数学の偏差値を上げて合格を目指す




中学数学 多項式 の教え方 展開の基本




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学
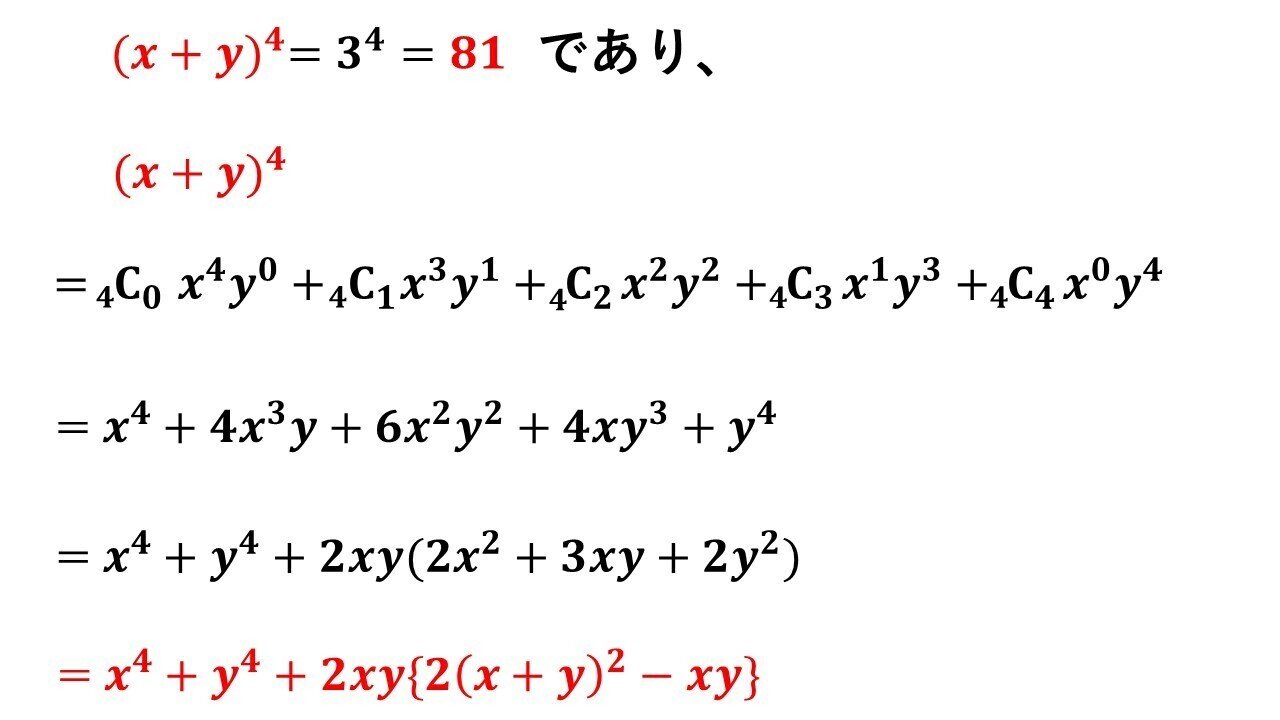



基本対称式の計算問題と二項展開 タロウ岩井の数学と英語 Note




展開 と 因数分解 の4つの基本公式




マクローリン展開 三角関数のマクローリン展開の計算 空間情報クラブ 株式会社インフォマティクス



数と式の問題 京極一樹の数学塾




N倍角の公式を表す多項式 チェビシェフの多項式 の係数の秘密 Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー



0 件のコメント:
コメントを投稿