面積体積 面積 の 単位 表 103421

角柱 V=Ah A底面積 h高さ 角すい V= Ah A底面積 h高さ 頭を切った角すい V= h(A1＋＋) A1,平行な底の面積 h高さ 直円柱 V=πr 2 h=r 2 h = πd 2 h=d 2 h M=2πrh=πdh r底面の半径 h高さ d底面の直径 斜切円柱 h1最大母線の長さ h2最小母線の長さ電話番号：02 ファックス番号：02 メールでのお問い合わせはこちら 村民のまめな暮らしガイドブック（R3年度版） くらしの相談窓口 便利な電話番号 年齢早見表（19年用） 鮫川村の郵便番号 度量衡換算表 (長さ・面積・体積・重量) 県南単位の間の関係 チャレンジシート① 学ぶ 1000 1 100 1 10 1 1辺の長さ 1cm 10cm 1m 10m 100m 1km 正方形の 面積 1㎠ 1㎡ 100㎡ 1a ㎡ 1ha 1㎢ 立方体の 体積 1㎤ 1mL 1dL 1000㎤ 1L 1㎥ 1kL 長さと面積・体積 重さと体積 1000倍 1000倍 1000倍 1000倍 1000倍

1

面積体積 面積 の 単位 表

面積体積 面積 の 単位 表- まずは証明の前に，球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です： 球の表面積： 4 π r 2 4\pi r^2 4πr2 →「心配アール二乗」 球の体積： 4 3 π r 3 \dfrac {4} {3}\pi r^3 34 πr3 →「身の上に表面積：体積とその熱との関係 生物学では、より広い表面積とより少ない体積が体を冷たく保つのに役立つと述べられています。 この現象を物理学的にどのように説明できるでしょうか。 ごめんなさい。 かっこいい。 表面積が大きいほど、体から出る

中学受験 単位変換を超簡単に 低学年でもできる９桁スライド図 かるび勉強部屋

求める体積は ＝352cm 3 。 表面積 直方体2本の表面積は （4×4×212×4×4）×2 ＝448cm 2 。 重なっている表面積は 4×4×22×4×4＝64cm 2 。 求める表面積は＝384cm 2 。しかく22,23がわかりません🙌🏻 面積は二乗、体積は三乗ってことはわかります。 中学生 数学 求め方を教えてください。 途中式を書いてもらえると助かります💦 お願いします。長さ、重さ、面積、体積の単位を相互に変換します。 例えば、長さで、5尺を入力すると、m、 『例えて言うなら日本刀の22倍』 と通常の変換のほか、例えも表示します。 また、重さを、300gを1500カラットへと変換すると、 『例えて言うなら、ミカンの23倍』 と出てきます。

長さ 面積 体積 1km 1km² 1km³ 1mm 1mm² 1mm³ 1cm 1cm² 1cm³ 1mL 1m 1m² 1m³ 1dL 1L 1a 1ha ⇔ x10 ⇔ x100 ⇔ x1000 ⇔ x10 ⇔ x100 ⇔ x100 ⇔ 1mm×1mm×1mm 1cm×1cm×1cm 1m×1m×1m 1km×1km×1km 1mm×1mm 1cm×1cm 1m×1m 1km×1km ⇔ ⇔ ⇔ ⇔ ⇔ ⇔ 10m×10m 100m×100m ⇔ 〇面倒でも赤矢印を飛ばしてはいけない。例：3m³をLに直すときは、半径と表面積で異なる単位の計算も可能です。 例：半径02m=表面積5024cm 2 計算をやり直す場合は「クリア」ボタンを押すと入力された数値が削除されます。 単位換算 一覧表 面積：ヘクタール と 平方キロメートル 面積：ヘクタール と 平方メートル 面積：ヘクタール と 平方センチメートル 面積：ヘクタール と アール 量・かさ・体積・容積：リットル と 立法メートル 量・かさ・体積・容積：リットル と 立法センチメートル 量・かさ・体積・容積：リットル と ミリリットル 量・かさ・体積・容積：リットル と

比表面積は一般に単位重量の粉体中に含まれる全粒子 の表面積の総和Sw(cm2/g)で 表わすが,単 位体積あた りの全表面積S,(cm2/cm3)で 示すこともある。 一発で覚える《単位換算》早見表｜超簡単1分で覚える換算表 長さの単位は 7マス 面積の単位は 11マス かさの単位は 7マス 重さの単位は 10マス マスの数を覚えておくと単位表を思い出しやすいですね。現行単位系の換算表 長さおよび距離 体積（容積） 体積・面積/公式集 立体の体積（v）、および側面積（m） 国際単位の換算表 ＜ご注意＞ 公用、商用に耐える正確さを保証しておりません。

日本の単位 尺貫法 換算一覧表 面積 長さ 距離 体積 重さ Origami 日本の伝統 伝承 和の心

1

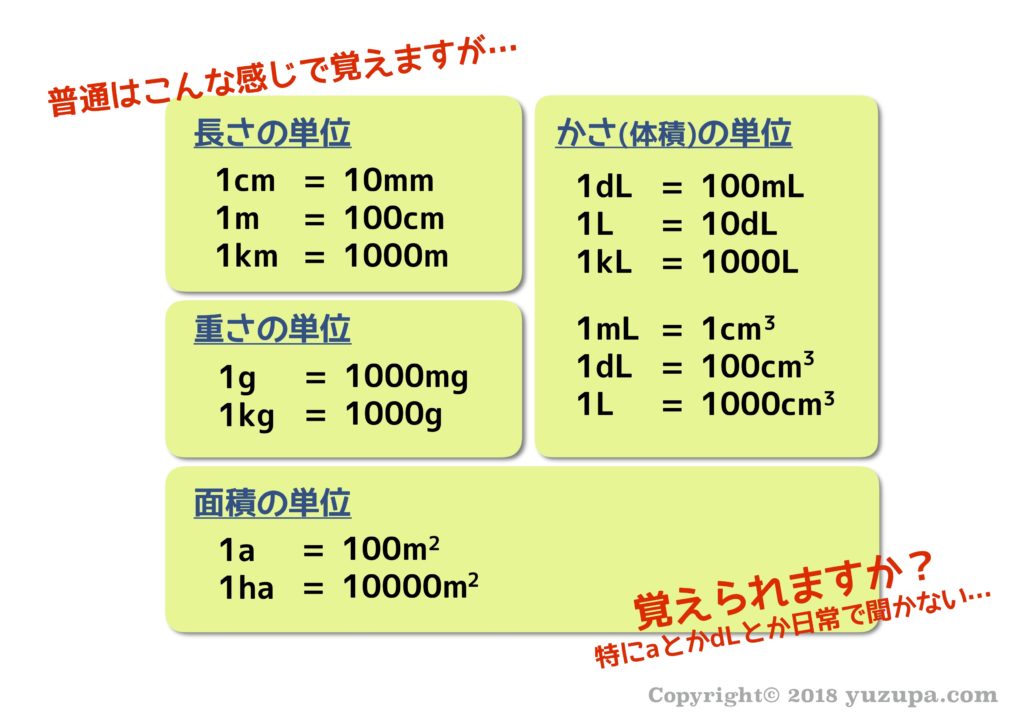
半球台の半径と高さから体積と表面積を計算します。 円環体の体積 円環体の体積 円環体（ドーナツ型）の内半径と外半径から体積と表面積を計算します。 楕円体の体積 楕円体の体積 楕円体の3方向の各半軸 から体積と表面積を計算します。・正四面体の表面積から1辺 正四面体の1辺の長さ・体積を表面積から計算します。 正四角錐 ・正四角錐(底辺と高さ) 正四角錐の体積・表面積を底辺と高さから計算します。 ・正四角錐(底辺と斜辺) 正四角錐の体積・表面積を底辺と斜辺から計算します。「 長さの単位 」に関しては 1km=1000m 1m=100cm 1cm=10mm の3つは絶対に覚えていなければいけません。 これは、日常見聞きするので小学4、5年生になれば、ほとんどの子どもがわかっているでしょう。 「 面積の単位 」に関しては 1a(アール)＝100m 2 1ha

小学生の算数の単位の覚え方は 単位換算表や変換のしくみ 体積 容積の違いも解説 学びtimes

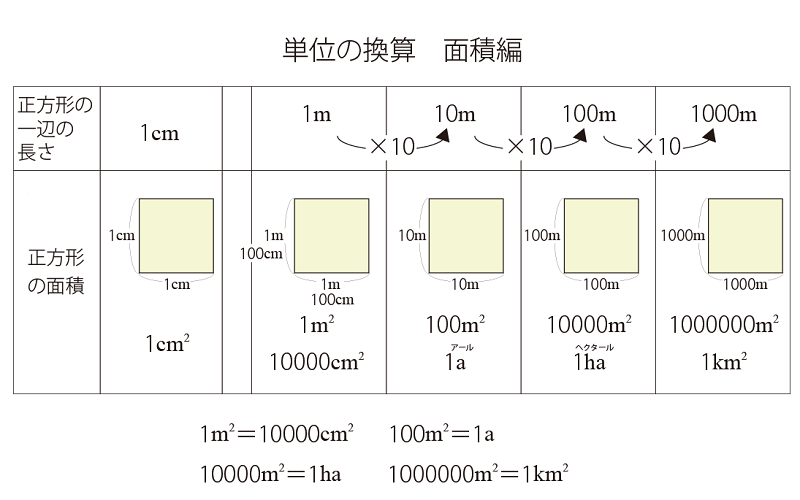
算数 単位の換算 面積編 はこうやって覚えよう 恋する中高一貫校 適性検査 徹底攻略

表面積対体積比は、 表面積対体積比およびさまざまに示されるsa / vol またはSA：V は、単位体積あたりの表面積の量です。 オブジェクトまたはオブジェクトのコレクションの。固体材料を含む化学反応では、表面積と体積の比率が反応性、つまり化学反応が進行する速度にとって重要な要素です。ここからは体積を学んでいきたいと思います。体積は表面積と違って簡単です！ 公式があるのでしっかり覚えていきましょう！単位が「cm²」ではなく「cm³」なので注意してください。 「柱の体積＝底面積×高さ」 で求めることができます。粒子の形状が球の場合は， φ v ＝ π/6，φ s ＝ π であり，立方体なら φ v ＝ 1，φ s ＝ 6 (ただし，立方体の1辺を D p として) となる．φ v および φ s は，同じ粒子でも，粒子径 D p のとり方によって異なってくる．また，粒子の単位体積当たりの表面積

長さ面積体積の単位まとめ 家庭学習レシピ

算数 単位表 時間 長さ 重さ 驚きの価格が実現 体積 容積 早見表 面積 即日受取可

A = 面積 P ＝ 円周(近似式) 円錐 V = 体積 A = 円錐面積 r ＝ d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 小学算数単位（メートル法、長さ・重さ・面積と体積／容積の単位、早見表付き） 学習ポスター＆クイズテスト＆やってみよう！ ｜ちびむすマンスリー学習ポスター・テストクイズ3ステップ学習 算数, 学習, 小学校 算数 小学算数単位（メートル法、長さ・重さ・面積と体積／容積の単位、早見表付き） 学習ポスター＆クイズテスト＆やってみよう！ 面積や体積の場合基準は m2 m 2 （平方メートル）や m3 m 3 （立方メートル）で、これに m m （ミリ）や c c （センチ）、 k k （キロ）などがつきます。

単位換算の計算プリント 面積に関する単位 の問題 全15回分無料 算数パラダイス

中学受験 単位変換を超簡単に 低学年でもできる９桁スライド図 かるび勉強部屋 中学受験 勉強 中学 勉強

動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru径r で微分すると表面積 の式となることに気付い た。または，それ以外の 球の体積と表面積の関係 に気付いた。 問1はできなかったが，問2において 半径 r の増加分 dr が十分小さいとき であれば，その際の体積の増加分 dV は表面積S(r)を用いてLiczba wierszy 33 bd ≡ 1 in × 1 ft = 7741 92×10 −3 m² boiler horsepower equivalent direct radiation bhp EDR ≡ (1 ft²) (1 bhp) / (240 BTU IT /h) ≒ 174 m² サーキュラーインチ

単位換算問題がわからない 小学生算数 覚え方がこれでわかる

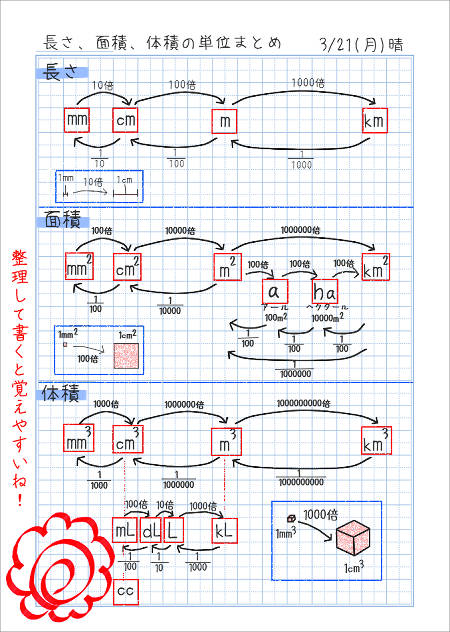
長さ面積体積の単位まとめ 家庭学習レシピ

  このピンは、あーみーさんが見つけました。あなたも で自分だけのピンを見つけて保存しましょう！具体例で学ぶ数学 > 図形 > 円柱の表面積と体積を求める公式 最終更新日 円柱の体積 V は、 円周率× 半径 × 半径 × 高さ 円柱の表面積 S は 2 ×円周率× 半径 × 半径 ＋ 2 ×円周率× 半径 × 高さ このページでは、円柱の表面積について詳しく説明2 比表面積の定義 比表面積は単位重量の粉体中に含まれる全粒子の表 面積の総和Sw(cm2/g) であらわすのが普通であるが, 単位体積あたりの全表面積Sv(cm2/cm3) で示すこと もある ここで単位体積というのは粉体の見かけ体積

Shurey S Macintosh Software

19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

円錐台の体積 拡底部の円錐台状の箇所に入れるコンクリート量を計算しました。 大変使いやすかったです。 植木鉢の土の量を計算するために使わせていただきました。 円錐台の側面積を求めたかったから。 円周率をπと表示できるようになるとミニム（米） min ≡ 1/480 US fl oz = 1/60 US fl dr = 0061 611 519 921 875 mL ダッシュ (dash)（米） ≡ 1/96 US fl oz = ½ US pinch = 0308 057 599 609 375 mL ダッシュ（英） ≡ 1/384 gi (Imp) = ½ pinch (Imp) 球の表面積・・・4πr² r³を微分すると3r²になります。 つまり、球の体積を微分すると円の表面積の公式になります。 そもそも微分とは、『少しの増加の間の変化量』を表現しています。 円の面積のちょこっとの増加分は円の周りの長さに相当します。

単位の換算表 メートル法 尺貫法 ヤードポンド法

体積の測定 測定のことを 即 知りたい ソクシリ キーエンス

これを具体的に説明してみようと思います。 まず、頭の中に1辺が1センチのサイコロを1つ思い浮かべてみて下さい。 そのサイコロの体積は、もちろん「1立方センチメートル」ですよね。 面積は、というと、6つの面があるのですから、「6平方センチメートル」です。 単位がついていると面倒なので、単位を除くと、 体積1 ： 表面積6 ということですね。 では

小６ 算数 小６ ４１ 量の単位のしくみ Youtube

Fdk3a7ctb5192box5b Com Es All Mt Unit All Poster Html

Lcm3 1oocm3 Barcm3 Sqrt Descubre Como Resolverlo En Qanda

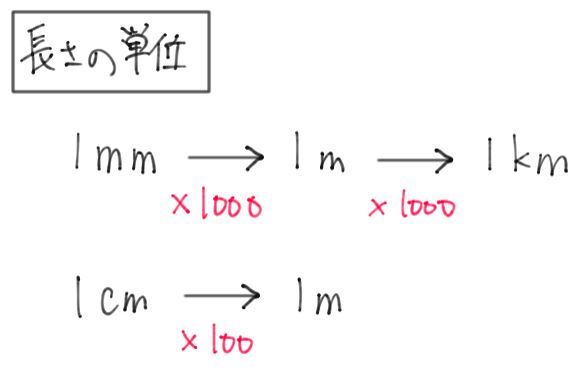
これで単位換算は簡単 単位の暗記術 後編 中学受験プロ講師ブログ

長さ 重さ 広さ 面積 容量 体積 の単位早見表 4thsight Xyz

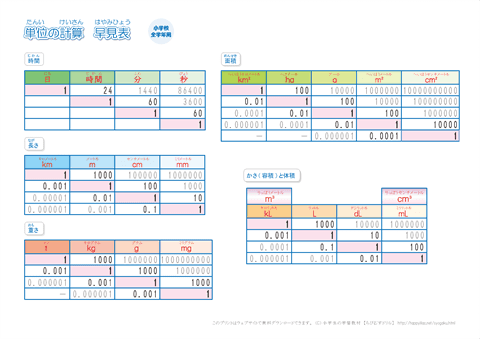
小学生用 算数の単位換算表 ちびむすドリル 小学生

Dfrac8002 5 10ml10am100m Descubre Como Resolverlo En Qanda

Fdk3a7ctb5192box5b Com Es All Mt Unit All Poster Html

小学生 算数の単位換算表を無料ダウンロードできます ちびむすブログ

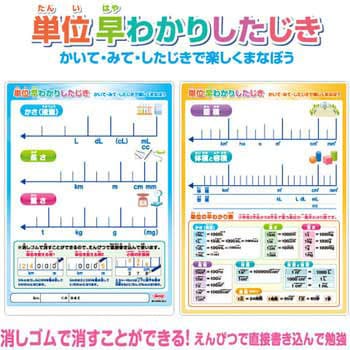
単位早わかり下敷 B5判 共栄プラスチック 下敷き 通販モノタロウ No 00 B5 4

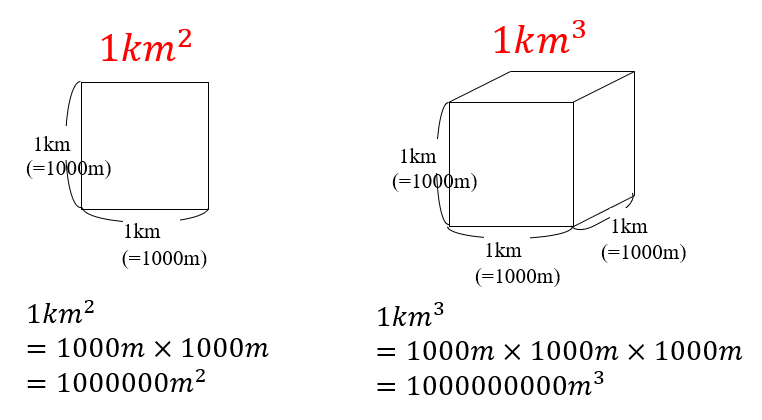
小学校算数で習う 単位 の覚え方 重さ 長さ 面積 体積 容積 数学fun

立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム

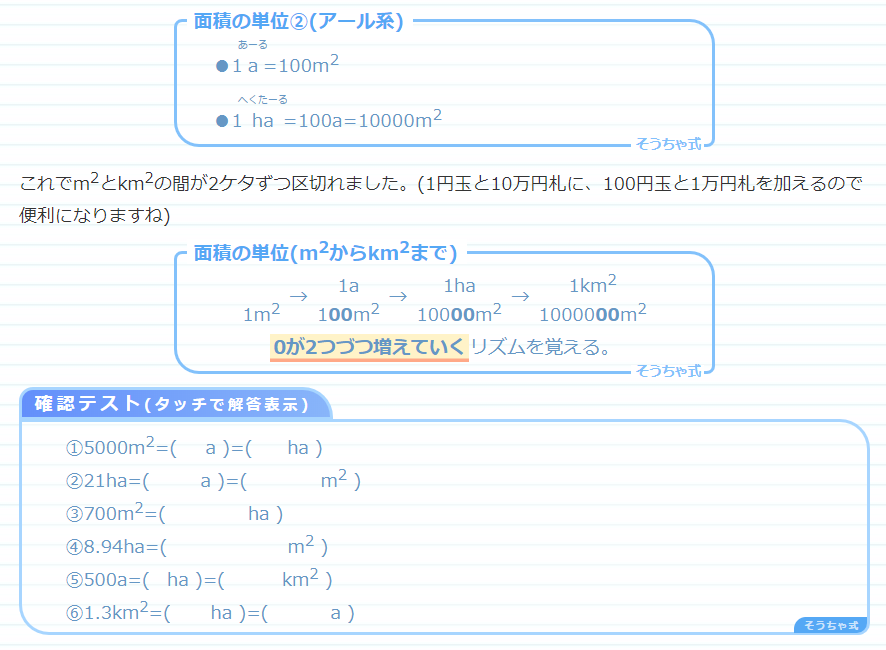
単位の総まとめ 重さ 長さ 面積 体積などの言葉の意味から直し方 計算問題まで そうちゃ式 分かりやすい図解算数 別館

算数 単位表 時間 長さ 重さ 面積 容積 体積 早見表 即日受取可 雑貨 その他 Omena 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト

小学校算数で習う 単位 の覚え方 重さ 長さ 面積 体積 容積 数学fun

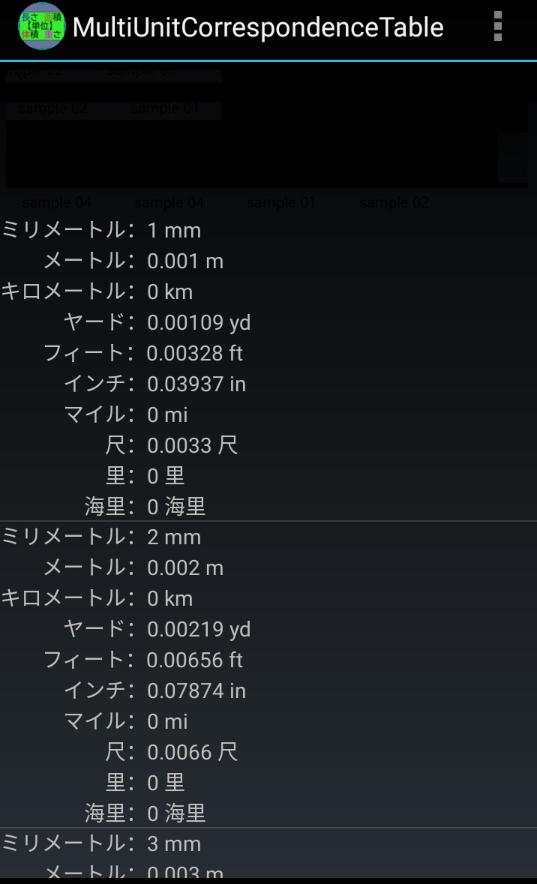
Android용 長さ 面積 体積 重さ単位変換一覧 Apk 다운로드

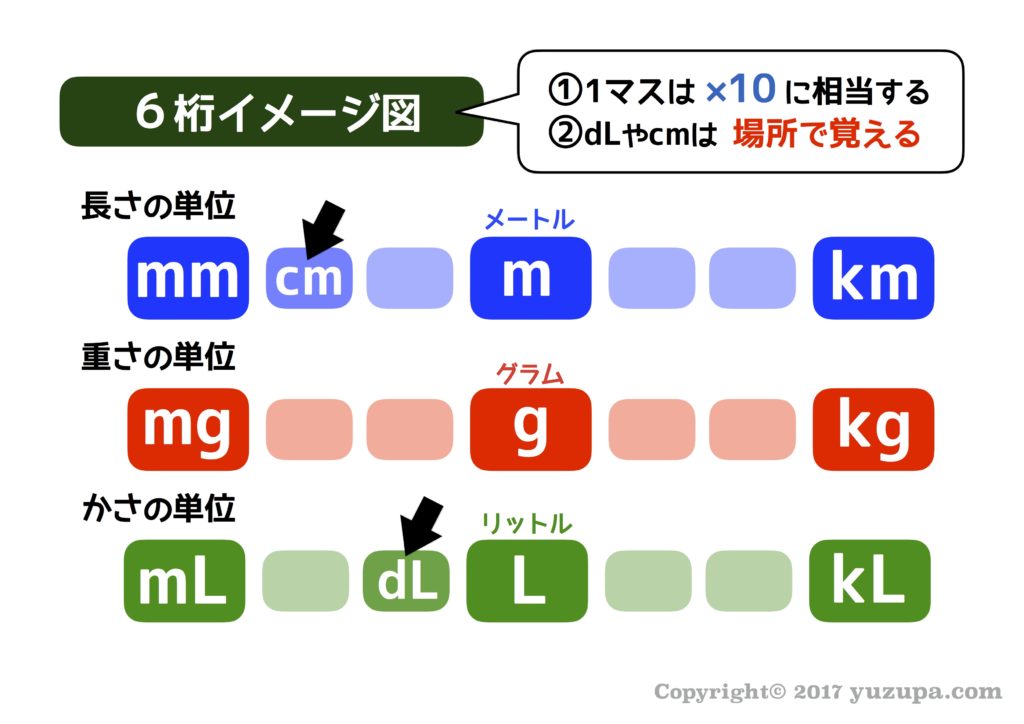
中学受験 単位変換はイメージ記憶で簡単に攻略 かるび勉強部屋

優雅 かさ の 単位 表

ヤフオク 単位換算の中古品 新品 未使用品一覧

度量衡 単位換算の早見表 長さ 距離 尺貫法 無料印刷pdf 計算問題無料印刷 Origami Project

算数の公式 教育 プリントアウトファクトリー Myricoh

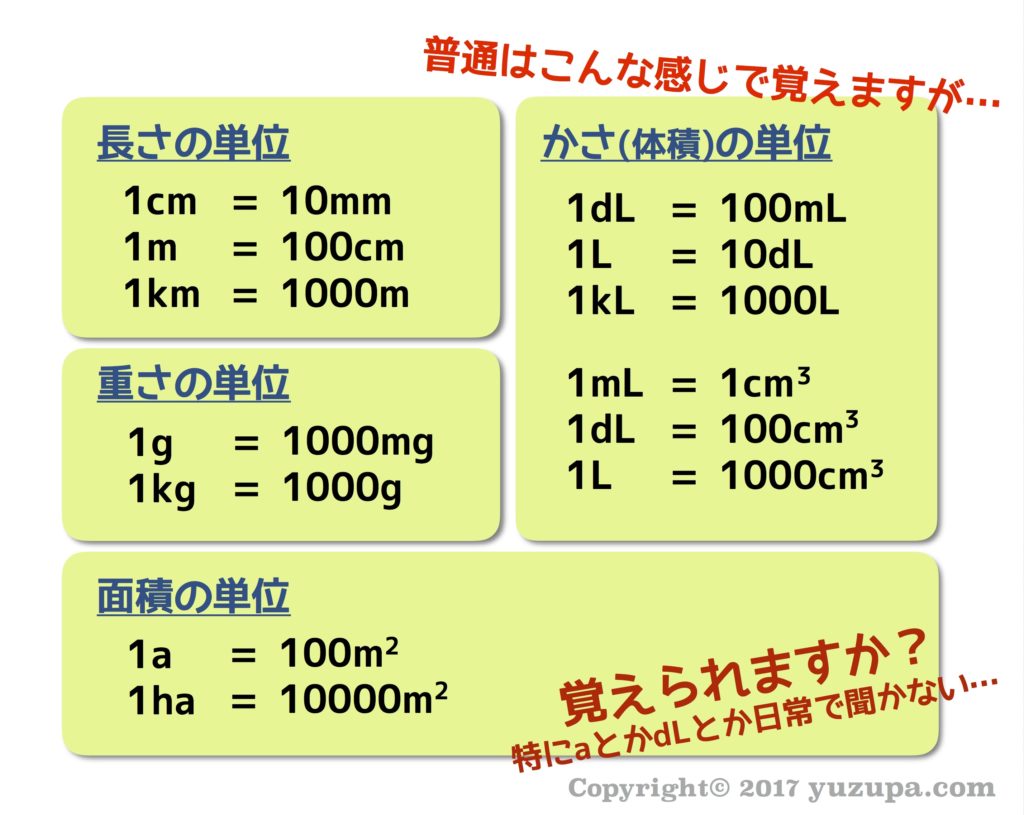
中学受験 単位変換はイメージ記憶で簡単に攻略 かるび勉強部屋

Fdk3a7ctb5192box5b Com Es All Mt Unit All Poster Html

単位換算 Stores

1

Descubre Como Resolverlo En Qanda

単位のきまり Youtube

Android 用の やさしい算数の単位換算表公式集02 Apk をダウンロード

算数で習う 単位の種類 35種類 一覧表 重さ 長さ 面積 時間 かさ 体積 容積 Yattoke 小 中学生の学習サイト

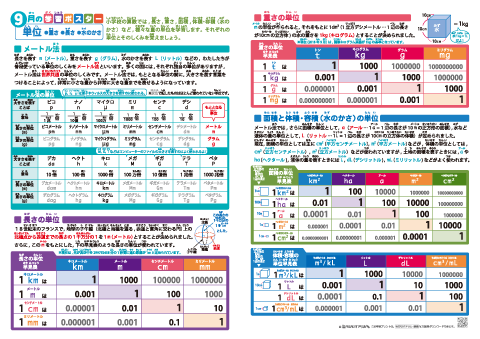
小学算数 単位 メートル法 長さ 重さ 面積と体積 容積の単位 早見表付き 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート ３ステップ学習

小学4 5 6年生の 単位をおさらいできる本 学習書 辞典 図鑑 小学学習参考書 Kumon Shop

小学生用 算数の単位換算表 無料ダウンロード 小学生の学習教材 ちびむすドリル 小学校 算数 単位換算表 算数

球の体積と表面積 公式と計算問題と証明 Irohabook

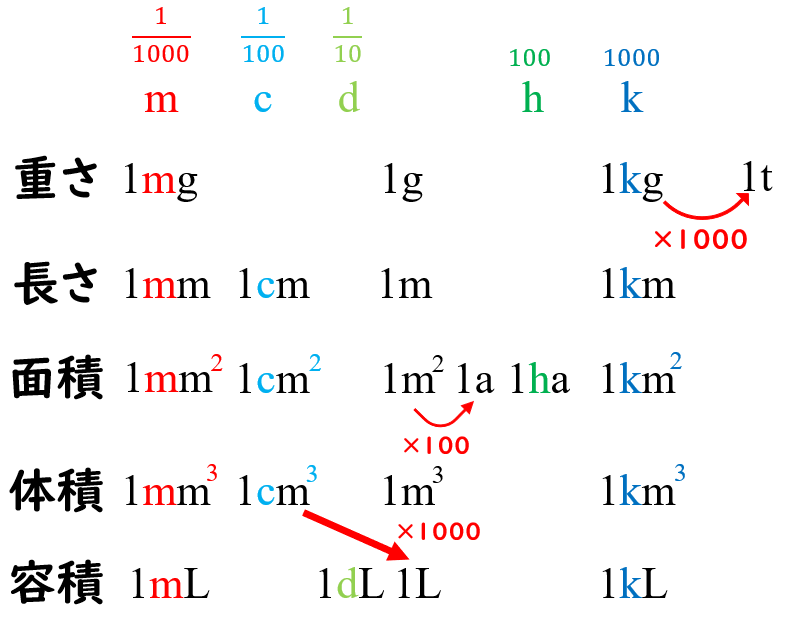
小学校算数で習う 単位 の覚え方 重さ 長さ 面積 体積 容積 数学fun

中学受験 単位変換を超簡単に 低学年でもできる９桁スライド図 かるび勉強部屋

単位早見表 教育 プリントアウトファクトリー Myricoh

算数 単位表 時間 長さ 重さ 面積 容積 体積 早見表 即日受取可 雑貨 その他 Omena 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト

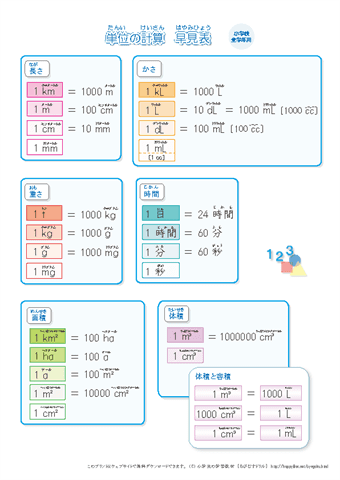
小学生用 算数の単位換算表 ちびむすドリル 小学生

小学校６年間で習う 算数の公式一覧 無料学習プリント 計算問題無料印刷 Origami Project

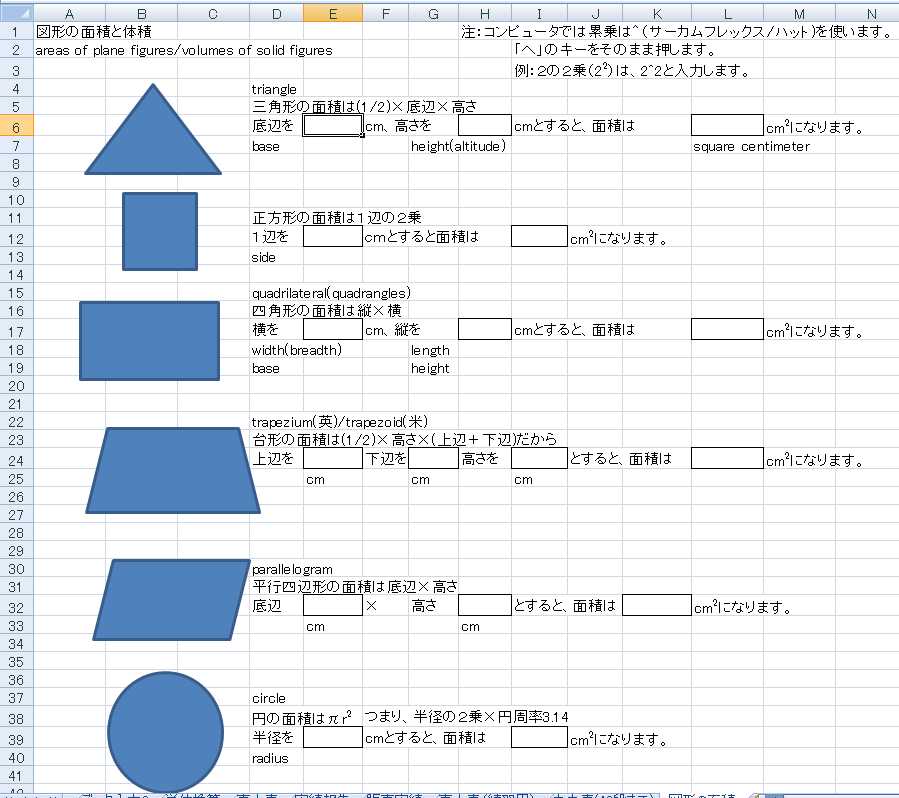
図形の面積と体積 しるぼの独り言

楽天市場 学習参考書 問題集 小学校 面積 体積の単位 学び考房

作ったことありますか 単位の換算がひと目で分かる 手作り単位計算尺 にtwitter民から 懐かしい の声 ねとらぼ

楽天市場 学習参考書 問題集 小学校 面積 体積の単位 学び考房

算数 長さ 面積 体積の単位をサッと換算できる覚え歌 キロキロとヘクトデカけたメートルがデシに追われてセンチミリミリ

体積の単位 算数 数学が好きになりmath

算数 長さ 面積 体積の単位をサッと換算できる覚え歌 キロキロとヘクトデカけたメートルがデシに追われてセンチミリミリ

単位の関係 長さと体積 Youtube

Amazon Co Jp 単位換算定規 文房具 定規 単位 換算 面積 体積 物の長さ 重さ 液量 知育玩具 小学生 算数 文房具 オフィス用品

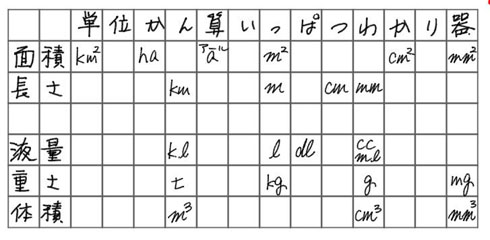
作ったことありますか 単位の換算がひと目で分かる 手作り単位計算尺 にtwitter民から 懐かしい の声 ねとらぼ

Amazon Co Jp 単位換算定規 文房具 定規 単位 換算 面積 体積 物の長さ 重さ 液量 知育玩具 小学生 算数 文房具 オフィス用品

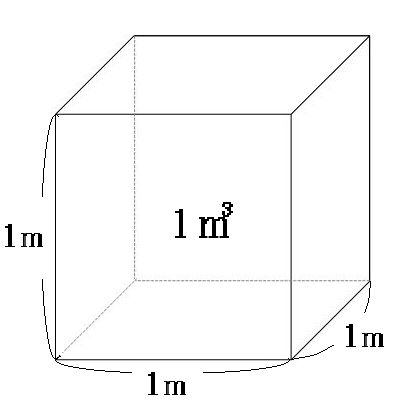
単位変換のやり方を解説 単位のかえ方 体積 かさ 時間 速さ

面積 体積の単位とそのしくみ 小学生 算数のノート Clear

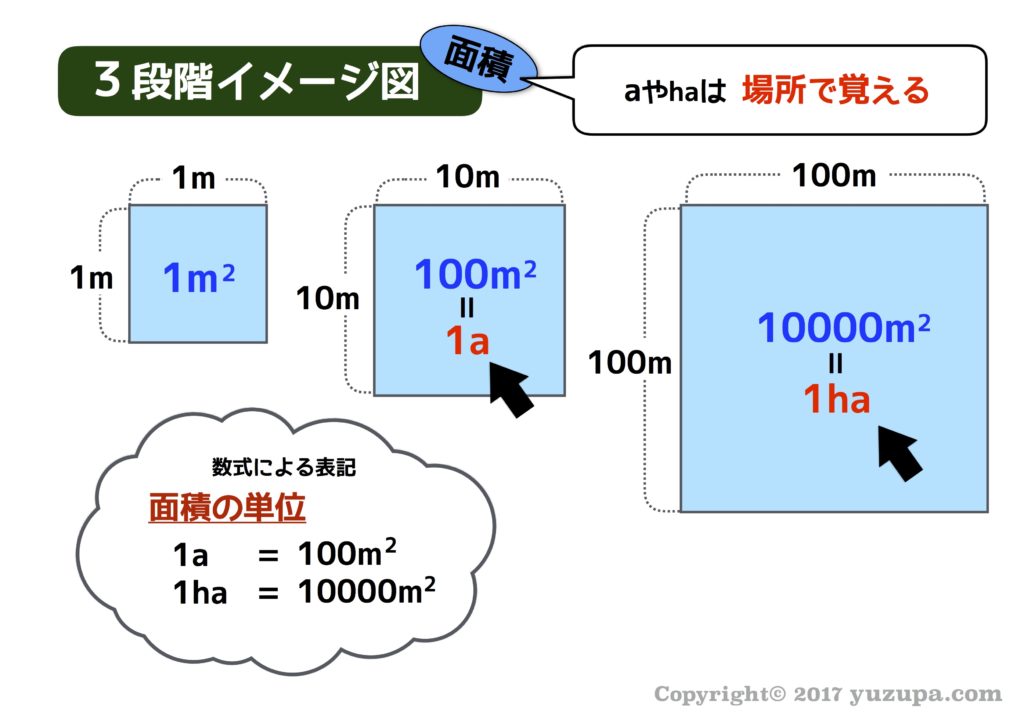
中学受験 単位変換はイメージ記憶で簡単に攻略 かるび勉強部屋

小学生 算数の単位換算表を無料ダウンロードできます ちびむすブログ

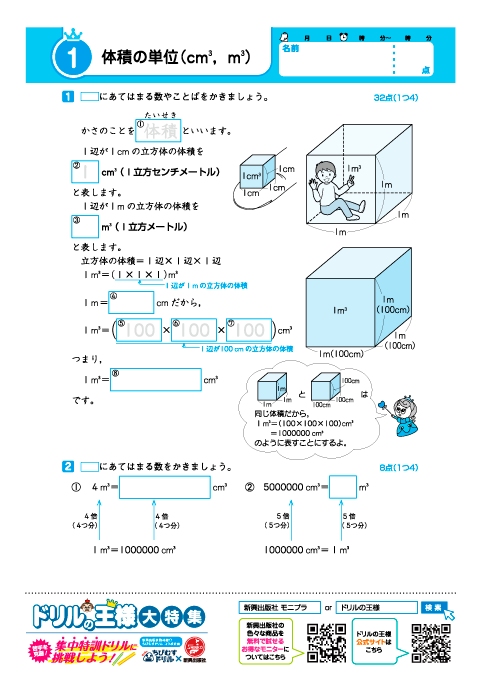
算数ドリル ５ ６年のとっくん 単位 無料ダウンロード ドリルの王様 大特集 リニューアル前 ドリルの王様 楽しく取り組めるから長続き 苦手対策にも 新興出版社啓林館 ちびむすドリル コラボ企画

一発で覚える 単位換算 早見表 長さ 面積 体積 かさ 重さ 小学算数 中学受験 Yattoke 小 中学生の学習サイト

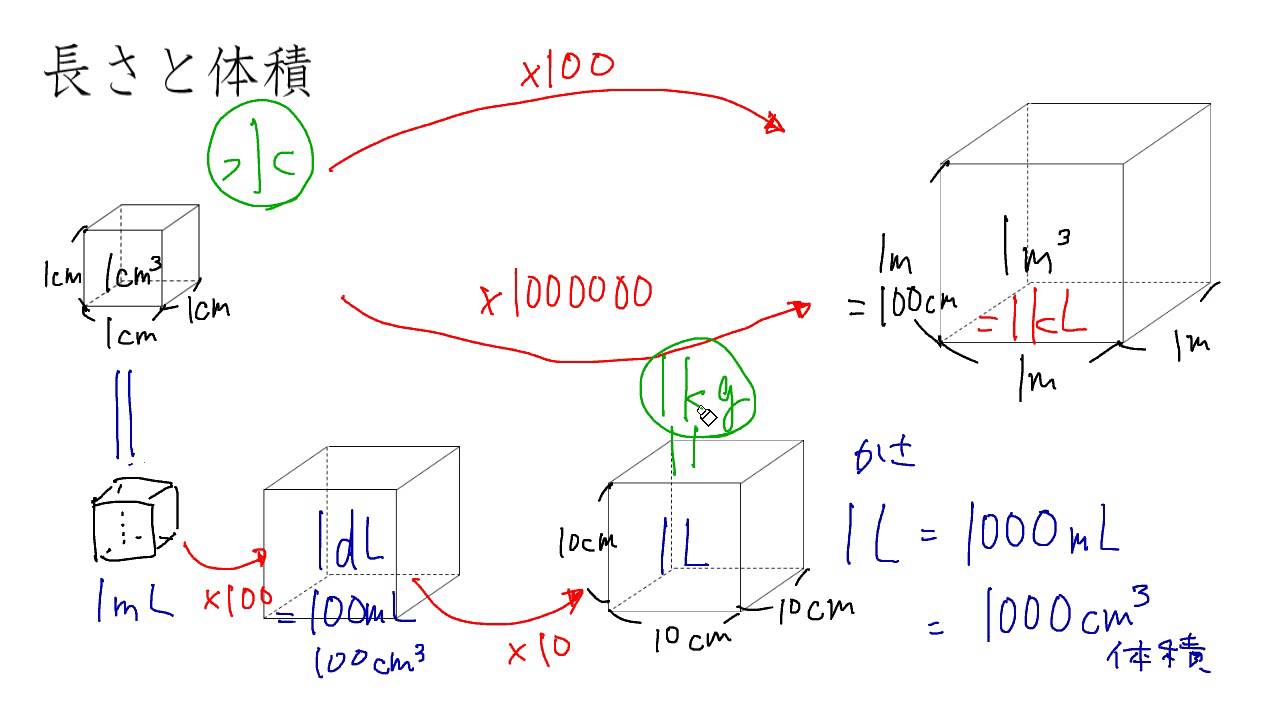
小学校６年算数 11 4 単位の関係 体積と重さ Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト

小学生の算数の公式一覧 面積や割合など苦手単元の対策法やおすすめ教材まで解説 学びtimes

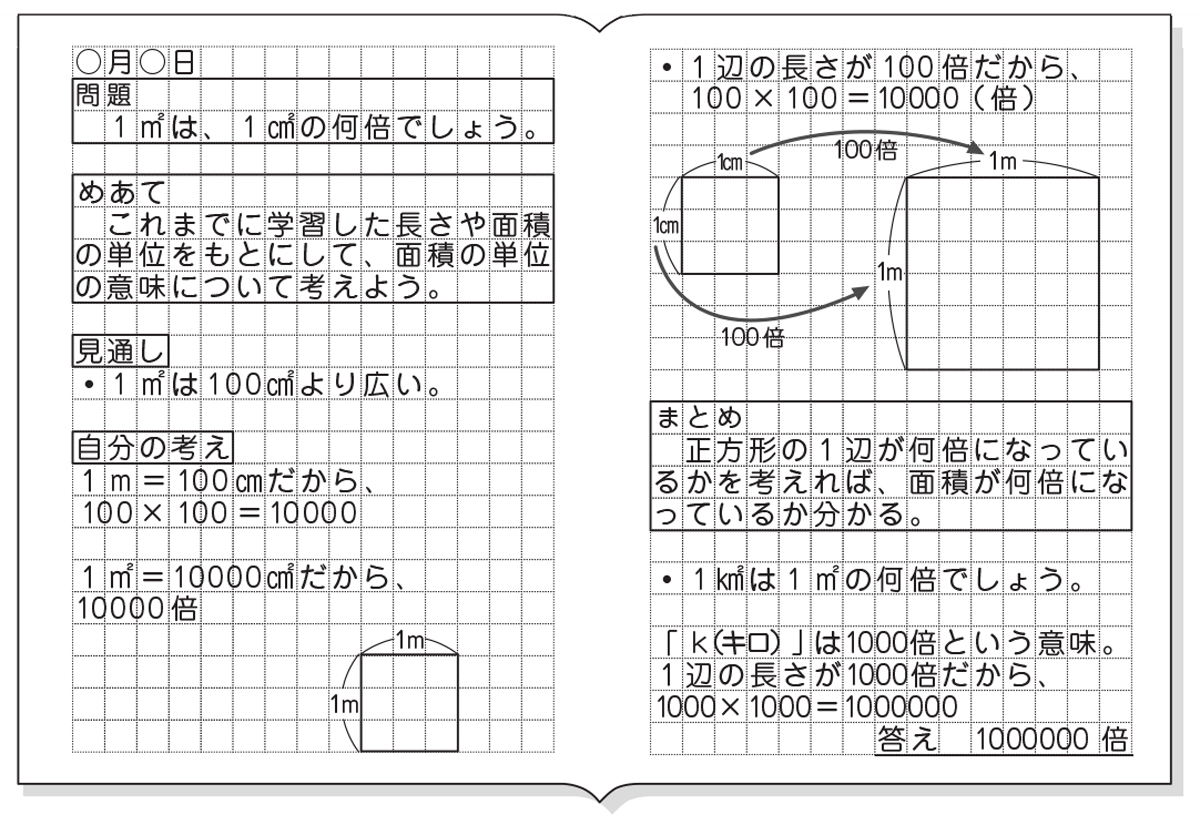
小6算数 量の単位 2 指導アイデア みんなの教育技術

授業案 算数２ ６年 単位変換の苦手な子への４つの対応 Teacher S Job

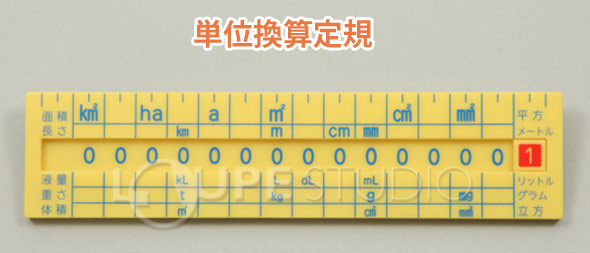
単位換算定規 文房具 定規 単位 換算 面積 体積 物の長さ 重さ 液量 知育玩具 小学生 算数 ルーペスタジオ

Ten Tokyo Shoseki Co Jp Shin Shido File 5nen 19 02 Pdf

授業案 算数２ ６年 単位変換の苦手な子への４つの対応 Teacher S Job

小学校算数で習う 単位 の覚え方 重さ 長さ 面積 体積 容積 数学fun

Si単位と組立単位 次元 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

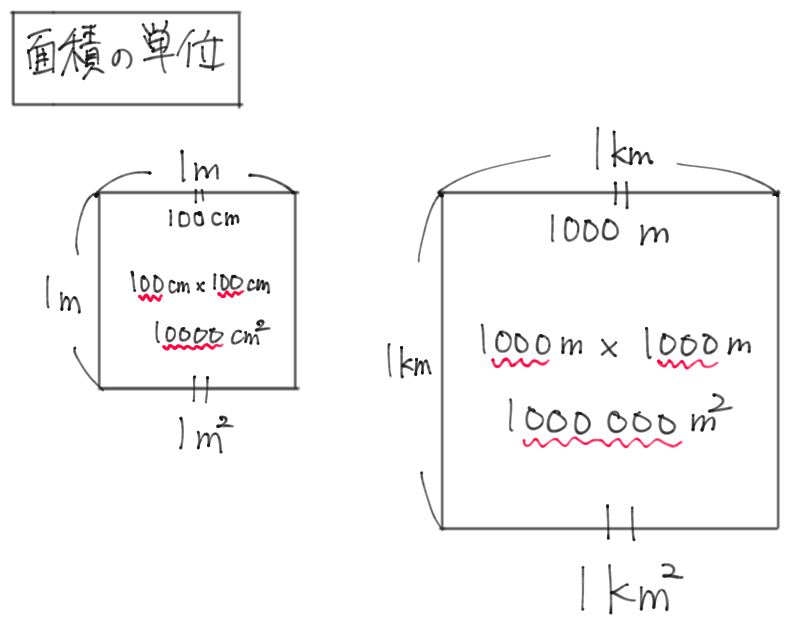
これで単位換算は簡単 単位の暗記術 後編 中学受験プロ講師ブログ

長さ面積体積の単位まとめ 家庭学習レシピ

3

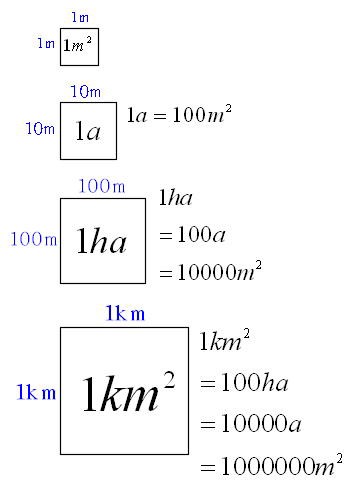
Mathematics メートル法と単位 働きアリ

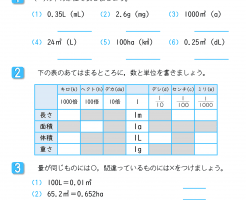
算数６年 の記事一覧 すきるまドリル 無料学習プリント

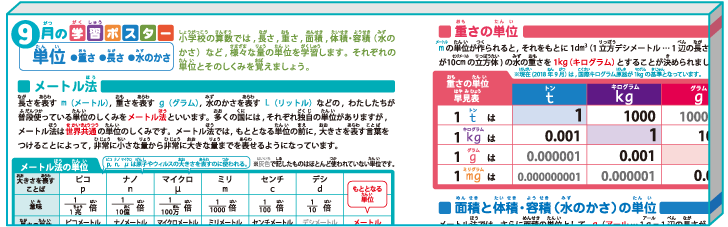
小学算数 単位 メートル法 長さ 重さ 面積と体積 容積の単位 早見表付き 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート ３ステップ学習

体積 体積の単位の関係 01 Youtube

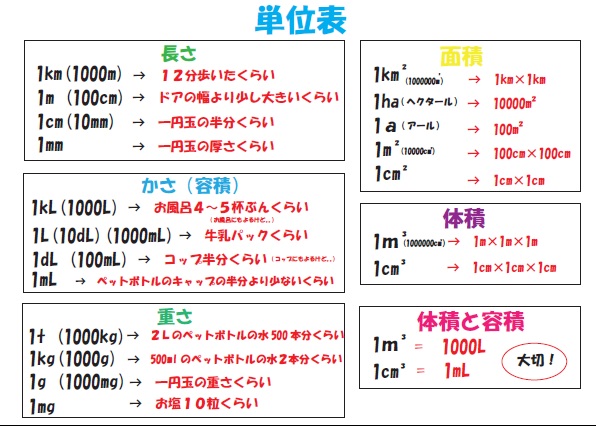
単位表 ブリッジぷりんと

坪 単位プラス 大日本図書

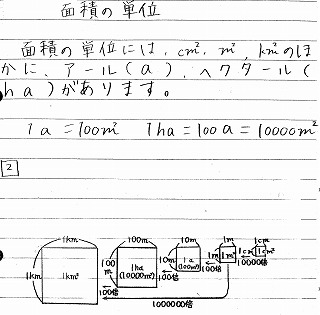
Tossランド 向山型算数基本型ノート 小６ いろいろな単位

度量衡 単位換算の早見表 広さ 面積 尺貫法 無料印刷pdfと畳数対応表 計算問題無料印刷 Origami Project

分からないので教えてください Clear

尺貫法の単位と換算一覧表 寸 尺 帖 坪など 無料印刷pdf 計算問題無料印刷 Origami Project

単位換算定規 文房具 定規 単位 換算 面積 体積 物の長さ 重さ 液量 知育玩具 小学生 算数 ルーペスタジオ

小学校算数で習う 単位 の覚え方 重さ 長さ 面積 体積 容積 数学fun

単位の関係 長さと面積 Youtube

1

小学生 算数の単位換算表を無料ダウンロードできます ちびむすブログ

1aは何 算数苦手な子に今させたい復習術 学校 受験 東洋経済オンライン 社会をよくする経済ニュース

体積と面積の違いは 1分でわかる違い 意味 公式と求め方

算数の教材 単位と図形集中学習4年 小学3 6年の図形と面積 体積 夢に向かって 23年中学受験日記

算数の単位を に 中学受験プロ講師ブログ

小学算数 単位 メートル法 長さ 重さ 面積と体積 容積の単位 早見表付き 学習ポスター クイズテスト やってみよう ちびむすドリル 小学生学習ポスター テスト 家庭学習シート ３ステップ学習 21 学習 算数 数学 勉強

Dfrac8002 5 10ml10am100m Descubre Como Resolverlo En Qanda

小学校算数で習う 単位 の覚え方 重さ 長さ 面積 体積 容積 数学fun